The cruel world...
在一切之前,把微小的工作尽可能做好吧。
该来的,总是要来的呢……
过了这么久,总算是下决心写一个较完整的介绍了啊……
这次要写的是,top tree 相关的东西究竟是什么,为什么说这东西实际上远强于 OI 中所流传的版本。
Top tree 最早由 Stephen Alstrup, Jacob Holm, Kristian de Lichtenberg 和 Mikkel Thorup 于1997年在 Minimizing Diameters of Dynamic Trees 作为 topology tree 的一个简化的接口给出,相比原来的更简单、更容易处理信息。稍后于2000年在 Maintaining Center and Median in Dynamic Trees 中命名为 top tree,完善了相关概念并给出了非局部搜索的应用。2003年在 Maintaining Information in Fully-Dynamic Trees with Top Trees 给出了一个全面的介绍。
如上所说 top tree 提出时是用 topology tree 实现的,而后者实现非常复杂,效率也非常低下。之后几年他们和 Werneck 和 Tarjan 给出了一些相对简单高效的独立实现。1998年 Holm 和 de Lichtenberg 在他们的硕士论文 Top-trees and dynamic graph algorithms 给出了最坏 $O(\log n)$ 的实现,但后来发现证明有错误。2005年 Tarjan 和 Werneck 结合路径分解的方法在 Self-Adjusting Top Trees 给出了均摊 $O(\log n)$ 的实现,并使用了另一种更简洁的描述。2006年 Werneck 在 Design and Analysis of Data Structures for Dynamic Trees 给出了基于收缩的最坏 $O(\log n)$ 的实现。
本文并不介绍 topology tree 等数据结构,一些相关的资料可在我以前的文章中找到。本文主要介绍 top tree 相关的东西究竟是什么,以及用 top cluster 的理论能干哪些事。((防跑路)做到其中的一些事可能并不需要实现 top tree。)包括一些自己想到的脑洞用法(
本文对 top tree 的描述主要基于 Werneck 和 Tarjan 使用的版本,这和 Alstrup 等人的是等价的,但应该会更好理解一些。
表示法
我们希望得到一种用于维护树上信息的数据结构,类似于用于维护序列信息的平衡二叉树。
平衡二叉树每次把序列中的 2 段合并为 1 段,所以可以考虑在树上用类似的做法,找出一类特殊的子树(或者说,一类特殊的连通子图)。两个这样的子树满足一定条件的话,可以合并成一个。最后即可将原树表示为一个合并结构,对每个合并出的子树记录一些子树内的信息,两个子树合并后的信息相当于合并两个子树的信息,最终合并出整个树的信息。
考虑我们设想的这类子树应该满足什么特殊要求。为了维护信息,我们希望这样的子树中只有不超过 2 个点和外部的点邻接,我们把这样的子树和 2 个指定的端点(endpoint)称为簇(cluster)。簇中非端点不和外部的点邻接。
簇代表了原树的一个路径以及一个子树,其中路径为两个端点之间的路径,而子树自然是直接忘掉对簇指定的 2 个端点即可。
显然,没有进行合并时,所有簇都是表示一个边,表示原树的一个边的簇称为 base cluster。
考虑以下两种操作,它们是树收缩(tree contraction)的两个基本操作,rake 消除一个度为 1 的点,compress 消除一个度为 2 的点,此外这些操作会把两条边替换为一条边。
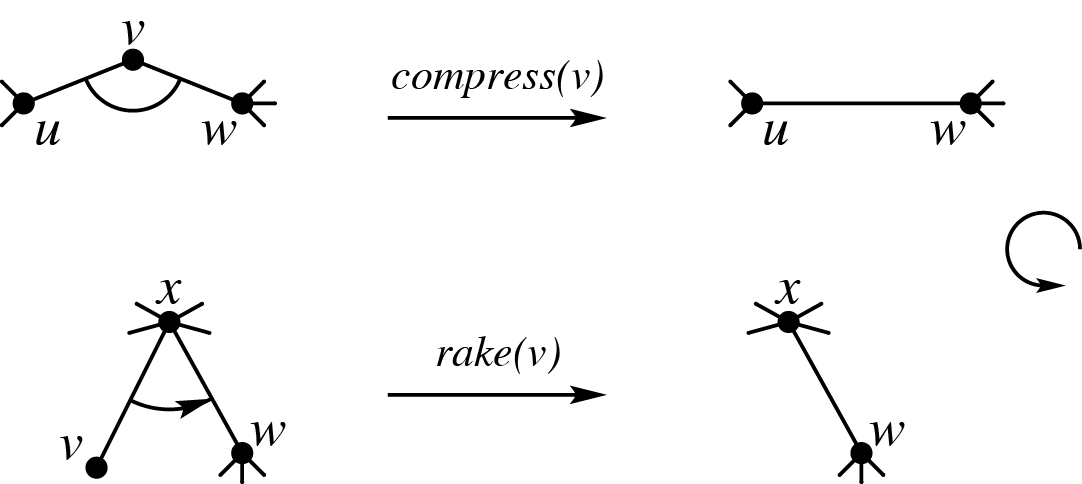
我们可以把这两种操作看作合并两个簇,显然这两个簇合并之后还是簇。合并后,簇中可能和外部邻接的点是图上新边的端点,所以可以认为这个簇表示新边,表示的边的端点也就是簇的端点。显然,这样就可以一直合并到只剩一个簇。
我们可以对树进行若干轮收缩,每轮收缩执行 rake 和 compress 的一个极大独立操作集合,这样 $O(\log n)$ 轮收缩后,树就只剩一条边了。最后这条边对应的簇称为根簇(root cluster)。
收缩过程中,簇的合并结构形成了一个树,我们把这个树称为 top tree。
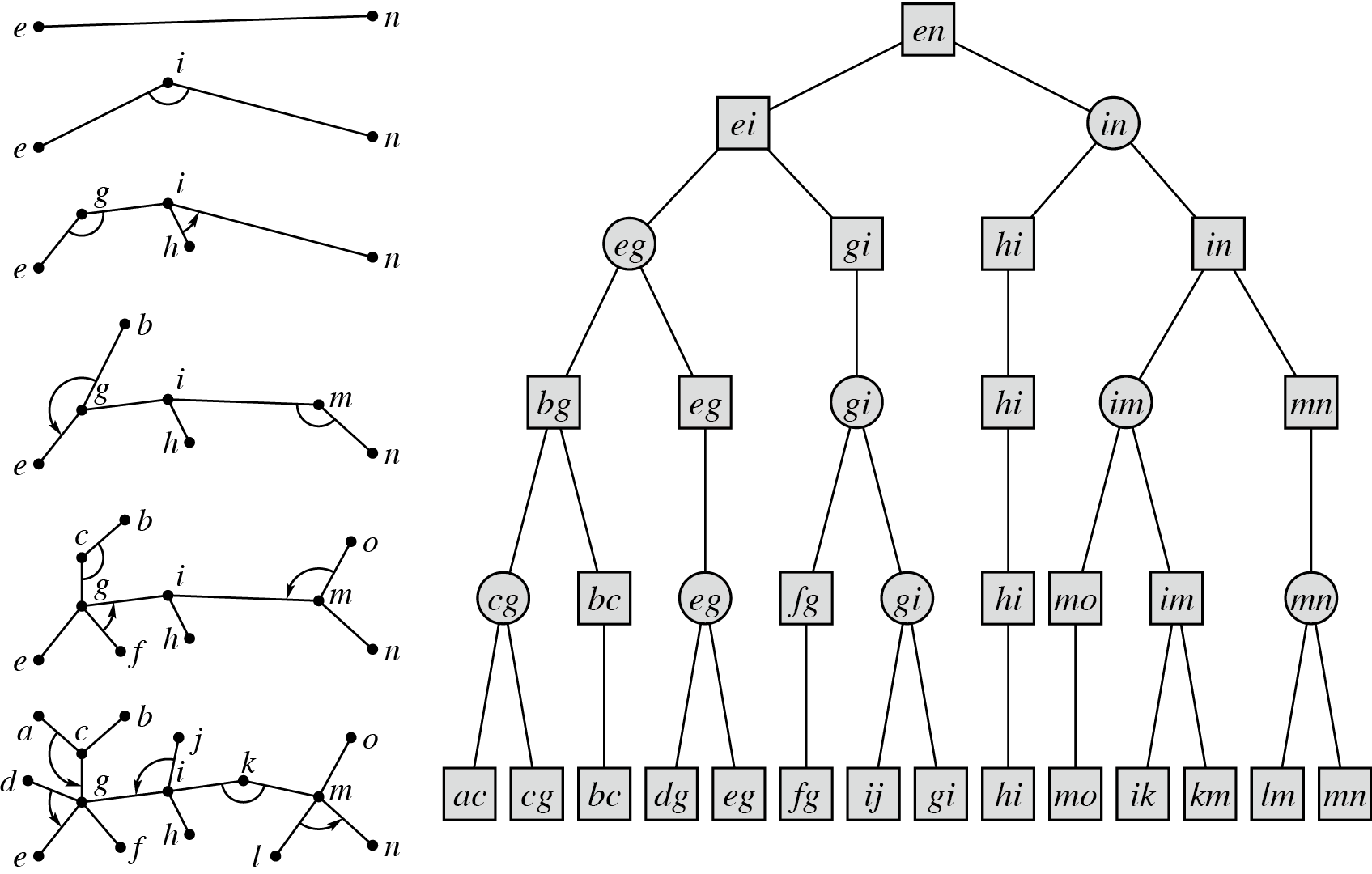
现在需要支持一些操作,如 $expose(v, w)$ 使根簇的端点变为 $v$ 和 $w$ (这在查询关于 $v$ 和 $w$ 的信息时需要用到),以及 $link$ 和 $cut$。但在介绍如何维护 top tree 之前,我们先考虑一下 cluster 和 top tree 能做什么事。
以下讨论关于某些点的操作时,我们认为这些点为根簇的端点(即这些点已经被 $expose$)。
维护动态信息
如上文所说,一个簇代表了原树的一个路径和一个子树。由 rake 操作合并的簇的路径是原簇之一所对应的路径,由 compress 操作合并的簇的路径是原来两个簇对应的路径的连接。而合并出的簇的子树则是原本对应的两个子树的并。维护路径和子树信息时,我们就可以对簇记录它对应的路径和子树的信息,在簇合并时合并它们。
关于边的信息储存在这条边对应的簇中,关于点的信息在消除这个点之后加入簇中(也就是说,簇内维护的信息,不包括端点上的信息),某种意义上这和平衡树类似。
类似序列上一些问题的做法,我们将会维护簇对应的路径和子树,以及两个端点相关的信息。
路径长度
方法显然。按照上图标号,compress 时 $(u, w)$ 对应路径长度为 $(u, v)$ 和 $(v, w)$ 之和,rake 时 $(u, w)$ 对应路径长度和未合并时的 $(u, w)$ 相同。
直径
对端点为 $v$ 和 $w$ 的簇 $C$ 维护 $\displaystyle maxdist_{i, j}(C)=\max_{\text{$x,y$ 为簇内点}\atop{(x=v \lor i=1)\land(y=w \lor j=1)}}dist(x, y)$ 即可。即维护簇路径长度,端点到簇内最远点距离,簇内最远点对距离。合并两个簇时,合并后簇 内部的最长路径长度 为 max(两个簇内的最长路径长度,公共端点发出的最长路径长度之和),compress 中端点发出的路径除了原来的,还可能会经过一个簇路径到另一个簇。
Sone1
需要支持
- 路径/子树 点权 加/赋值
- 查询 路径/子树 点权 sum/min/max
我们维护
- 簇路径/簇中除簇路径以外的部分 点权 sum/min/max
- 簇路径/簇中除簇路径以外的部分 点权 加/赋值 的 lazy propagation 标记
即可。
注意之前说到,簇内维护的信息,不包括端点上的信息。所以这里维护的 簇路径 点权 sum/min/max 不包括端点上的点权。
最大权独立集
维护簇的两个端点分别选和不选时的答案,对于 base cluster 端点都选答案为 $-\infty$,否则为 $0$。按之前所说,消除某点后计入这个点的权值即可。
「SDOI2017」切树游戏
维护簇的两个端点分别在和不在连通子树内时的方案数即可。为了快速转移,可以维护方案数的 Walsh-Hadamard 变换数组。
Query on a tree IV
类似直径,对端点为 $v$ 和 $w$ 的簇 $C$ 维护 $\displaystyle maxdist_{i, j}(C)=\max_{\text{$x,y$ 为簇内标记点或端点}\atop{(x=v \lor i=1)\land(y=w \lor j=1)}}dist(x, y)$ 即可。即簇路径长度,端点到簇内最远标记点距离,簇内最远标记点对距离。
Query on a tree V
相比前一题不需要维护 $maxdist_{1, 1}$,即簇内最远标记点对距离了。
Query on a tree VI
维护簇路径上点是否全为白/黑色 及 和端点连通(这里不考虑端点颜色是否相同)的白/黑点数即可。
Query on a tree VII
相比前一题再维护连通点集中最大权即可。
Jabby's shadows
1 号操作类似直径和 QTREE6 做法,维护簇路径上点是否全为白/黑色 及 簇路径长度,端点到连通的最远白/黑点距离,端点连通的最远白/黑点对距离即可。
为了完成 2 号操作,还需要维护把簇路径上全变为白/黑点后的信息,操作时直接赋值并打标记即可。
非局部搜索
对于一个性质,如果一个点/边在树中有这个性质,那么在所有包含它的子树中都有这个性质,我们就称这个性质是局部的。比如树中的最小点,在子树中同样是最小点。局部性质容易用 cluster 自底向上维护,而非局部性质似乎更有趣。
对于表示整个树的簇(即根簇)和一个有某非局部性质的点/边,如果将根簇分为两个簇,可以通过性质和维护的信息,选择点/边所在的子簇,那么就可以使用非局部搜索找到这个点/边。
考虑在 top tree 上二分,每次我们需要找到包含要找的点/边的孩子,但它们的性质需要在整个树中才能体现。
因此,我们用 2 个临时簇表示树中当前簇以外的部分,如果当前簇有 2 个孩子 $A$ 和 $B$,我们把它们和临时簇合并,得到 $A'$ 和 $B'$,它们合并后表示整个树。
所以我们只需要支持,对于一个根簇,选择包含要找的点/边的孩子,就可以用二分完成非局部搜索。
Lowest common ancestor & level ancestor
$v$ 和 $w$ 的最低公共祖先指最低的(即最深的)同时为 $v$ 和 $w$ 祖先的点,$v$ 的 $d$ 世祖指 $v$ 的深度为 $d$ 的祖先。
令 $jump(v, w, d)$ 为在 $v$ 到 $w$ 路径上从 $v$ 开始跳 $d$ 次的点,这可以用非局部搜索做到。那么以 $r$ 为根 $LCA(v, w)=jump(r, v, \frac12(dist(r, v)+dist(r, w)-dist(v, w)))$,$LA(v, d)=jump(r, v, d)$。
Center
对于一个有正边权的树 $T$,它的 center 指最小化 $\max_{w}dist(v, w)$ 的点 $v$。
显然可以通过维护任意一条直径,找直径的中点做到,但我们可以直接找到 center。
直接找的做法也是显然的,每次选择公共端点到簇内最远点距离更大的簇即可,正确性显然。
Median
对于一个有正点权和正边权的树 $T$,它的 median 指最小化 $\sum_{w}weight(w)\times dist(v, w)$ 的点 $v$。
Median 在 competitive programming 中通常被称为 centroid/重心。
我们知道对于一条边,如果一侧的点权和大于等于另一侧的点权和,那么这一侧有至少一个 median。容易推得每次选点权和大的簇即可。
Top cluster 分解
Topology tree 源于 topological partition,它表示了一个多层次 topological partition 结构。自然可以想到把树分解为 top cluster。容易证明对于 $n$ 个点的树可以分解为 $\Theta(n/z)$ 个大小 $O(z)$ 的簇。
也许这就是真正的树分块吧
Simple Tree
每个簇记下簇路径点权和,簇路径/簇中除簇路径以外的部分 点权 加 的 lazy propagation 标记 即可。取 $z=\sqrt n$ 时最优。
([TODO]:想不到适合的题了,暂时鸽了)
upd: lxl 和 ccz 基于这个技巧给出了一类树上邻域相关问题的解决方案,such as 「THUPC 2019」不用找的树。
$O(\sqrt m)$ 动态最小生成树
Topology tree 第一次出现就是用于解决这个问题。不难想到直接把做法中的 topology tree 换为 top tree。
用 top tree 维护当前的最小生成树,为了维护非树边,我们在点上附加一些 label 用于表示这个点发出的非树边,每个 label 也对应一个 base cluster,这样 top tree 的大小变为 $\Theta(m)$。还是只需要考虑如何完成删除树边,也就是找到最小的连接两个分量的非树边。类似 topology tree 的做法,将树分为 $\Theta(\sqrt m)$ 个大小 $O(\sqrt m)$ 的簇,并在这些簇上建一个 top tree。对 top tree 每层维护每对簇之间的最小非树边,这里非树边在一对簇之间当且仅当边对应的两个标记分别在这两个簇中。维护每对簇之间最小非树边的结构类似序列上的四分树,Frederickson 将 topology tree 做法的类似结构称为 2-dimensional topology tree。这样修改和查询都能在 $O(\sqrt m)$ 时间内完成,证明方法和四分树类似。
显然,和 topology tree 做法一样,top tree 做法可以用稀疏化(sparsification)技巧改进到 $O(\sqrt n)$。
Top tree 分治
这是我想到的一个脑洞用法,最早于下面第一个例题找到应用
Tree Query
显然点分治可做到 $O(n\log^2n+q\log^2n)$。
考虑在 top tree 上进行类似点分治的做法,每个簇存下簇内点到端点的距离并排序。自底向上归并即可减少 $n$ 上的一个 $\log n$ 因子。注意到查询过程类似用 range tree 做 orthogonal range searching 的过程,所以可以用 fractional cascading 减少一个 $\log n$ 因子。这样就得到了一个 $O(n\log n+q\log n)$ 的做法。如果允许离线的话,可以同时归并查询并统计答案。
瞎口胡的,并不知道有没有问题
([TODO]:想不到适合的题了,暂时鸽了)
upd: “全局平衡二叉树”对应一个深度为 $O(\log n)$ 的类似树收缩的结构,可以认为在上面的分治本质上是 top tree 上分治,可以在《IOI2019中国国家候选队论文集》中的《浅谈树上分治算法》找到一个应用。那个例子,常数个关键点的话显然可以定位到 log 个结点?那个例子,真的不应该放在维护动态信息?作者在其他地方写了一些其他的应用,文中似乎并没有提到。
关于实现
Self-adjusting top tree
2005年 Tarjan 和 Werneck 结合路径分解的方法在 Self-Adjusting Top Trees 给出了一个非常像 ST-tree(aka link-cut tree)的 self-adjusting 实现。
首先指定一个度为一的点为根,并将所有边定向到它,这样的树称为 unit tree。然后将树分解为不交叉的、边不相交的路径,其中每个路径开始于一个叶子、结束于另一个路径,除了一条 root path(或 exposed path)结束于根。
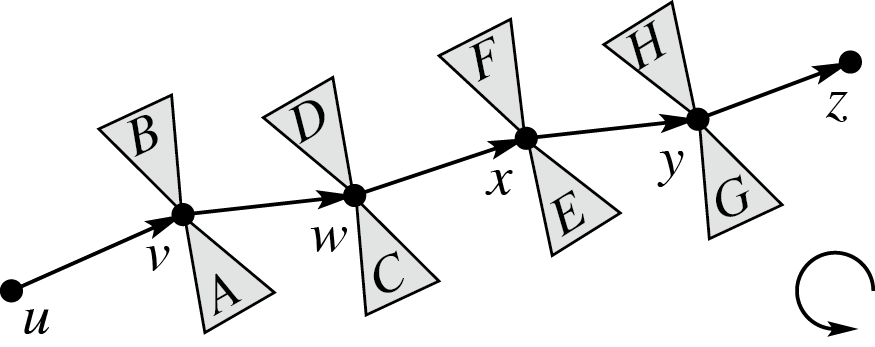
现在需要得到表示整个树的簇,簇路径为 root path,注意到 root path 以外的部分是很多根在 root path 上的 unit tree,所以我们递归地将它表示为一个簇。
我们把 root path 上每个点两侧的这些簇分别 rake 为 1 个,再将它尽可能晚地 rake 到路径上,即在这个点被 compress 前。
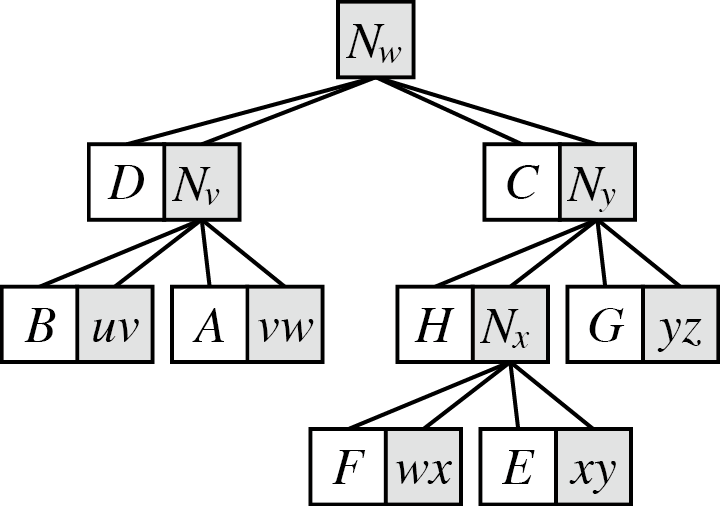
我们用一个 augmented top tree 表示这个过程。表示某点某一侧的 rake 的结点在 augmented top tree 中形成了一个树,称为 rake tree。每个表示 compress 的结点最多可能有 4 个孩子,其中 2 个表示两侧 rake 到路径上的簇,2 个表示这次被 compress 的簇,所以实际最多可能表示 2 次 rake 和 1 次 compress。同样这些结点也形成了一个树,称为 compress tree。
以下是一个完整的例子,右侧为实际表示的 top tree。
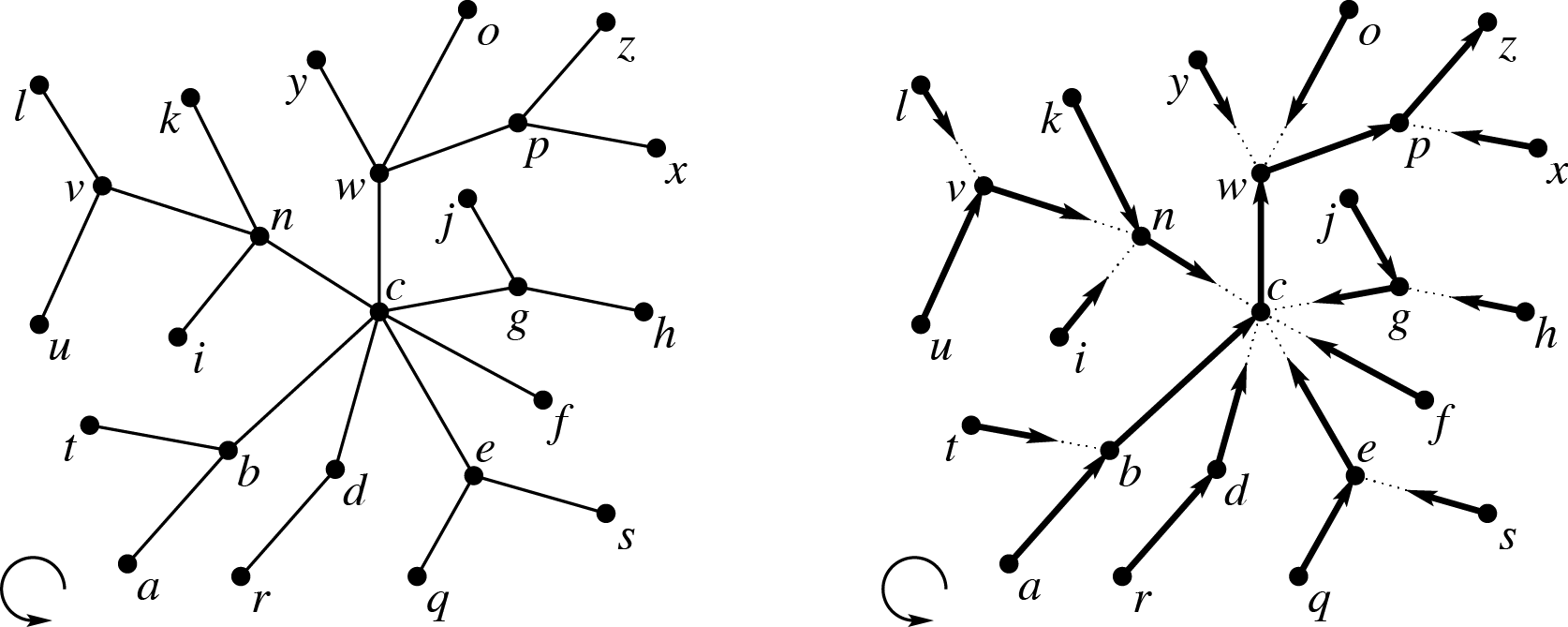
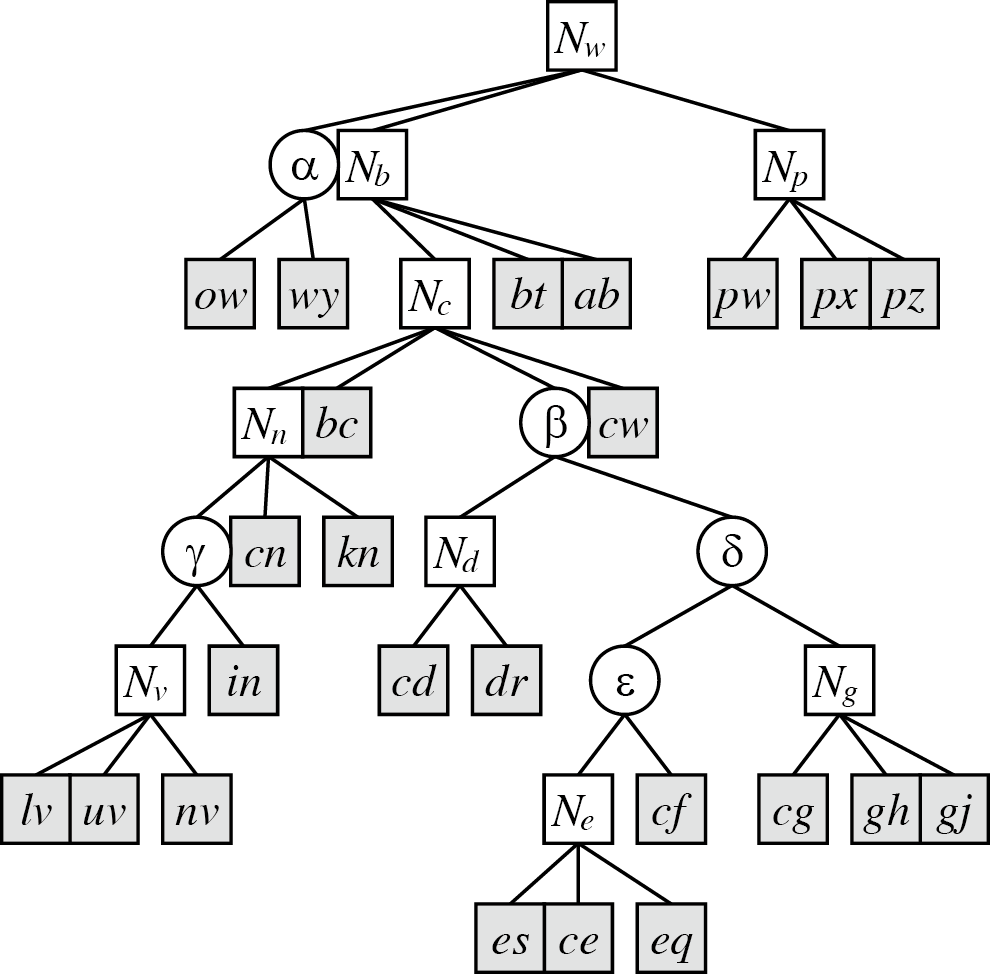

仅考虑 compress tree 的话最后的结构类似 ST-tree,rake tree 可以认为是用于维护虚子树信息。
我们发现 compress tree 和 rake tree 上的点也是可以旋转的,所以可以用 splay tree 维护。为了完成 $expose$,我们需要先实现 $soft\_expose$,即令希望 $expose$ 的两点在 root path 上。类似 ST-tree 的 $expose$,也是进行 local splay、splice、global splay,即若干次 compress tree 和 rake tree 上的 splay,若干次 splice 使点在 root path 上,最后在表示 root path 的 compress tree 上进行一次 splay 即可。
通常 $soft\_expose$ 并没有使两点成为根簇的端点,做到这需要 $hard\_expose$。首先仍是进行 $soft\_expose$,然后 splay 出表示两点之间路径的簇,再临时改为将路径两侧的簇(如果有的话)rake 到表示两点之间路径的簇上。$link$ $cut$ 和 $hard\_expose$ 类似,也是先进行 $soft\_expose$,再讨论几种情况即可。
以上内容可能有不少细节,具体参见原文。
常数实际也没那么大,原文分析的界很松,即使这样也为 $12\log n$ 倍旋转常数,相比之下 ST-tree 为 $6\log n$ 倍旋转常数,两篇文章分别认为旋转常数为 $8$ 和 $2$,实际差距并没有那么大,Dynamic Trees in Practice(ACM Journal of Experimental Algorithmics (JEA) 版)中的测试显示通常常数为 ST-tree 的 3~4 倍(当然,根据应用时的数据特性和实现会有所不同)。
实现时可以类似 ST-tree,原树中每个点都有对应的 compress tree 上的点,这样相当于每个点都会在 compress tree 被消除并将对应信息加入,不需要在 rake 的时候加入端点信息了。
如果不需要维护边的顺序,可以把 compress tree 上的点改为 3 叉。
在一些不需要维护边的信息的应用中可以省略 base cluster。
对于一些应用(如之前的应用例子 最大权独立集 和 「SDOI2017」切树游戏 可以省去 rake tree,此时和 ST-tree 几乎一致。(但我们现在会用 cluster 那套理论了:))
为了操作方便,还可以把 rake tree 也改成 3 叉的,只有中孩子是一个 compress tree 的根,但这样维护信息的常数可能会大一些。
我的实现只有 $link$ $cut$ 之类操作的讨论比较麻烦,如果不要求分解为极长路径可以解决这个问题,但 $expose$ 时会很麻烦,希望能找到一个比较好的解决方案。
Contraction-based top tree
1998年 Holm 和 de Lichtenberg 在他们的硕士论文 Top-trees and dynamic graph algorithms 、2006年 Werneck 在 Design and Analysis of Data Structures for Dynamic Trees 给出了基于收缩的最坏 $O(\log n)$ 的实现。
如之前所说,我们对原树进行若干轮收缩,每轮收缩执行 rake 和 compress 的一个极大独立操作集合,这样可以得到 $O(\log n)$ 层的收缩结构。直接实现即可 $O(n)$ 时间建树,但我们还需要考虑如何完成 $link$ $cut$ 和 $expose$。
首先,我们对每层维护一个 Euler tour,每层对于所有点维护一个指针指向这个点发出的一个弧。对 Euler tour 中每个弧维护指针指向它的后继、前驱和方向相反的弧,这样即可判断是否满足 rake 或 compress 的条件。
$link$ $cut$ 时对每一层考虑,首先删除需要删除的簇,再加入需要加入的簇,判断是否有的收缩操作变得无效,最后进行新的收缩操作直到收缩极大。细节参见原文 3.3。
虽然高度为 $O(\log n)$ 很显然,但并不容易证明 $link$ $cut$ 操作时间为 $O(\log n)$ (即每层只会影响到 $O(1)$ 个簇),原文用了很长的篇幅去证明这一点。
$expose$ 有 2 种实现方法。一种是直接重建原收缩,这只需要强制两个点不被收缩即可。
另一种可以认为是把包含这 2 个点为内部结点的簇(即消除这 2 个点的簇及它们的祖先)全部删去,剩下 $O(\log n)$ 个根簇形成了大小 $O(\log n)$ 的树,对这个树建一个临时 top tree 即可。由于只是临时的而且大小为 $O(\log n)$,所以并不需要建 Euler tour 和保证平衡。不就是像线段树/平衡树一样定位到 log 个结点嘛
(脑洞用法)第 2 种实现方法令人联想到一类问题,这类问题的操作和树中 $k$ 个点相关。用类似的方法可以在 $O(k\log n)$ 时间内得到 $O(k\log n)$ 个簇形成的树,还可以进一步收缩为 $O(k)$ 个簇,或许常数要比传统做法好一些。(可能在一些维护不可快速合并的信息的问题上有应用?($k=2$ 的情况似乎在 动态平面图边双连通性 中有应用))
此外还有一种做法是不实现 $expose$,直接在簇上操作(类似线段树和一些平衡树的做法),这样常数远小于 $expose$。
Contraction-based top tree 常数是比较大的,而且没有 splay tree 带来的好处。但在单纯的维护可快速合并的信息之外的一些问题上,可能是不可替代的(如 $O(\sqrt m)$ 动态最小生成树)。
并没有完整实现过 contraction-based top tree,也不知道应该怎么实现比较好,希望能找到一个比较好的实现。
静态树
一些应用不需要支持 $link$ $cut$ 操作,这时候我们有更简单的实现方案,并且常数更小。
显然可以直接建 top tree,并不再需要支持动态部分的东西了。我们也可以类似 self-adjusting top tree 的方法,结合路径分解实现。具体来说,我们建一个类似 self-adjusting top tree 的结构,和最坏 $O(\log n)$ 的 ST-tree 相似,为了保证树高,我们需要使用重路径分解,每个 compress 子树 和 rake 子树 是一个静态的 biased dictionary problem(ST-tree 则需要解决动态的问题)(即要求访问 BST 内点 $v$ 所需时间为 $1+\log\frac{\sum_wweight(w)}{weight(v)}$)。有一种做法是建 compress tree 时每次在当前簇中选一个点,使子簇不超过簇的一半大小,rake tree 上情况类似。
有些时候类似的做法在中国 competitive programming 中被称为“全局平衡二叉树”。
上文提到了“ST-tree 则需要解决动态的问题”。正是因为当时出现了 biased tree,解决了这个问题的动态版本,最早的 ST-tree 才可以做到最坏 $O(\log n)$。显然静态版本更早就被解决了。
一些其他问题
使用 top cluster 分解时可能需要重编号,如果实现不当会导致严重的 cache miss。
和前面一样,我的关于它的实现也不是很优美,希望能找到更好的实现。
一些没有提到的东西(想起来什么就在这里补充)
我还曾考虑过把这套理论用在仙人掌上,在树收缩基础上增加合并两个端点相同的 cluster 的操作,得到的似乎也是个功能非常强大的东西。
然而以前写的介绍有大量的错误,包括我当时以为某个名字有人使用过,后来才发现是另一个东西。再后来也没(gū)什(gū)么(gū)时(gū)间(gū)重新整理那套理论了。
没有 rake tree 的版本是非常容易实现的,功能也几乎和上面一样强大。可以参考我在 动态仙人掌 I~III 的提交。

 鄂公网安备 42010202000505 号
鄂公网安备 42010202000505 号